更新日:2023年2月27日

- 目次
- そもそも判断推理とは?
- まずは「数的処理」を知ろう
- 判断推理とはどんな問題?
- 判断推理の対策は? どんな戦略で取り組む?
- 主な職種の判断推理の出題数
- 【過去問からの問題例】判断推理の解き方
- (問題1) 位置関係
- (問題2) 真偽
- (問題3) 立体図形の分割・構成
- 判断推理の効果的な勉強方法
- 方法① 解法の定石をマスターする
- 方法② 頭の中だけで考えず、書き出すことも大切
- 方法③ どんどん演習を重ねる
- まとめ
そもそも判断推理とは?
今まで判断推理の問題を解いたことのないみなさんに、判断推理に対するイメージをつかんでいただき、今後の指針を示していきます。
まずは「数的処理」を知ろう
教養試験の中で、最も多く出題されているのが数的処理です。数的処理は、「判断推理」「数的推理」「資料解釈」の3分野に分類されますが、図形分野を独立させて、「判断推理」「数的推理」「図形」「資料解釈」の4分野に分類されることもあります。受験案内に、「数的処理(判断推理・数的推理・資料解釈)」と記載されていることもありますが、この場合も、判断推理、数的推理の中に図形分野を含めたことになっていますので、図形分野も出題されていることに気をつけてください。数的処理の出題内容の基礎は、小学校の算数、中学校の数学レベルで、おおむね高校受験レベルですが、場合の数、確率、図形などは、高校1年生の数学Ⅰ・数学Aの内容も問われています。
判断推理とはどんな問題?
判断推理は、「論理」「真偽」「対応関係」「試合」「数量推理」「順序関係」「位置関係」「暗号」「操作手順」「推理」という内容に分かれます。これまで、耳馴染みのない単元名もあったかもしれませんが、算数パズル、論理パズル的な内容をイメージしていただけるとわかりやすいかもしれません。
判断推理の問題の多くは、条件が5~7個程度与えられていて、そこから確実にいえることを探し出すというものが多く、論理的な思考力が問われているといえます。条件が多いとどの条件から手をつけたらよいかという苦労もありますし、反対に条件が少ないときは、ヒントが少ないという苦労もあります。
そして、図形を含めた判断推理は、「立体図形」「展開図」「軌跡・移動」「図形の分割・構成」に分類されます。こうした問題は、算数、数学ではあまり問われていなかったものも多いです。解法が明確に決まっている問題もありますし、ある程度の試行錯誤をしながら調べ上げていく必要のある問題もあります。特に立体図形は、平面の中ではイメージしにくいこともあり、苦手とされる方が多いです。
判断推理の対策は? どんな戦略で取り組む?
数的推理と比較すると、判断推理は算数、数学の知識はあまり多く必要とされません。ある程度、地道に調べ上げていくということが必要ですから、取り組みやすいとはいえます。しかし、場合分けが複雑になったり、手間がかかることが多いことも事実ですから、思考力を高めていくために、問題演習を重ねていくことが大切です。
主な職種の判断推理の出題数
年度によって多少の変動が見られますが、最新の2022年度の判断推理の出題数は、以下のとおりです。おおむね、判断推理は、数的処理の半分くらいを占めており、教養全体という視点から見ても重要な科目といえます。なお、図形の内容も含めた出題数としております。
| 職 種 | 判断推理 | 数的処理合計 | 教養試験解答数 | 教養科目出題数 |
|---|---|---|---|---|
| 国家総合職 | 8問 | 16問 | 40問 | 40問 |
| 国家一般職 | 8問 | 16問 | 40問 | 40問 |
| 国家専門職 | 8問 | 16問 | 40問 | 40問 |
| 裁判所事務官 | 8問 | 17問 | 40問 | 40問 |
| 国立大学法人等職員 | 8問 | 13問 | 40問 | 40問 |
| 地方上級全国型 | 10問 | 17問 | 50問 | 50問 |
| 地方上級関東型 | 7問 | 12問 | 40問 | 50問 |
| 地方上級中部北陸型 | 10問 | 17問 | 50問 | 50問 |
| 東京都Ⅰ類B一般方式 | 5問 | 16問 | 40問 | 40問 |
| 特別区Ⅰ類事務 | 10問 | 19問 | 40問 | 48問 |
| 横浜市大卒事務 | 8問 | 17問 | 40問 | 40問 |
| 京都府行政A | 10問 | 16問 | 40問 | 40問 |
| 経験者採用 | 10問 | 17問 | 50問 | 50問 |
| 市役所B日程 | 8問 | 14問 | 40問 | 40問 |
| 市役所C日程 | 8問 | 14問 | 40問 | 40問 |
| 警視庁Ⅰ類第1回 | 9問 | 17問 | 50問 | 50問 |
| 東京消防庁Ⅰ類第1回 | 5問 | 15問 | 45問 | 45問 |
【過去問からの問題例】判断推理の解き方
ここまで、判断推理の全体像を見てきましたが、易しめの最新の2022年の過去問を通して、判断推理とはどのようにして解いていくのかという発想をお伝えしていきたいと思います。
(問題1) 位置関係
<2022年 裁判所事務官>
A、B、C、D、Eの5人が前を向いて横一列に座っている。以下は、異なる5人の発言である。
ア メガネをかけている人は、私の左隣に座っている。
イ 私の右隣にはCが座っている。
ウ 私から右に3番目にはAが座っている。
エ 私の左隣にはB、Bから左に2番目にCが座っている。
オ 私の左隣にはDが座っている。
5人のうち1人だけがメガネをかけているとしたら、それは誰か。
1:A 2:B 3:C 4:D 5:E
- 回答・解説を見る
-
(解 説)
図の左側を左方向として、発言者が不明なため、ア~オの発言者をア~オ、メガネをかけている人をメと記すことにします。アの発言:メ ア
イの発言:イ C
ウの発言:ウ ○ ○ A
エの発言:C ○ B エ
オの発言:D オまず、イ、ウ、エの3つの発言から、Aは最も右の位置に座ることがわかります。このとき、Cがウ、Aがエとわかることから、この時点で、以下の順序になることがわかります。
イ C 〇 B A
もし、Dがイの位置に座ったとすると5人の座った位置は次のようになります。
D C E B A
しかし、この場合はCがオとなってしまい、異なる5人の発言という条件に反します。したがって、イの位置に座ったのはEとわかり、5人の座った位置は次のようになります。
E C D B A
このとき、Bがオ、Eがイ、そしてDがアと決まり、ア(D)の発言から左隣のメガネをかけている人はCとわかります。
(正 解) 3
(問題2) 真偽
<2022年 特別区>
A~Eの5人が、音楽コンクールで1位~5位になった。誰がどの順位だったかについて、A~Eの5人に話を聞いたところ、次のような返事があった。このとき、A~Eの5人の発言内容は、いずれも半分が本当で、半分は誤りであるとすると、確実にいえるのはどれか。ただし、同順位はなかった。
A 「Cが1位で、Bが2位だった。」
B 「Eが3位で、Cが4位だった。」
C 「Aが4位で、Dが5位だった。」
D 「Cが1位で、Eが3位だった。」
E 「Bが2位で、Dが5位だった。」
1:Aが、1位だった。
2:Bが、1位だった。
3:Cが、1位だった。
4:Dが、1位だった。
5:Eが、1位だった。
- 回答・解説を見る
-
(解 説)
発言内容に出てくる2人の人物が一致しているBとDの2人の発言に着目します。
B:「Eが3位、Cが4位」
D:「Cが1位、Eが3位」
1つは本当でもう1つは誤りの内容であるため、Eが3位と決まります。
そして、Cは1位ではないため、Aの発言からBが2位となり、Eの発言からDが5位でなく、Cの発言からAが4位と決まります。
最後に、1位はCでなく5位はDでないため、Dが1位、Cは5位と決まります。
ここまでをまとめると、5人は次の順位であったとわかります。1位 2位 3位 4位 5位 D B E A C 以上より、Dが1位であったことは確実にいうことができます。
(正 解) 4
(問題3) 立体図形の分割・構成
<2022年 東京都Ⅰ類B(新方式)>
下の図のように、同じ大きさの小立方体27個を組み合わせた大立方体に八つの丸印をつけ、八つの丸印から大立方体の反対側の面まで垂直に穴をあけたとき、穴があいた小立方体の個数として、正しいのはどれか。
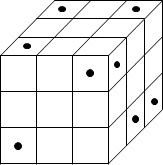
1:16個 2:17個 3:18個 4:19個 5:20個
- 回答・解説を見る
-
(解 説)
小立方体からできている大立方体の問題は、各段をスライスして、各段ごとに考えるとよいです。そこで、本問題も、各段ごとに穴があいた小立方体の個数を数えていくことにします。次の図の灰色の部分が穴をあけた小立方体です。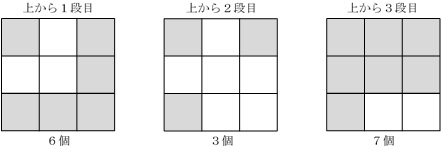
したがって、穴があいた小立方体の個数は、
6+3+7=16(個)
となります。(正 解) 1
判断推理の効果的な勉強方法
以上の問題で、判断推理のイメージはわかってきましたでしょうか?パズルを解く感覚とも似ています。
方法① 解法の定石をマスターする
判断推理には、さまざまなジャンルがありますが、解法の流れがはっきりしている問題があります。学習の初期は、そうした問題を数多く解いていくことが大切です。その際、丸暗記は避け、なぜそうなるのかということを意識しながら、理解するということが必要になります。理屈がわかってしまえば、機械的に解くことができる問題もありますから、解法のストックをどんどん増やしていきましょう。
復習の際は、問題を何も見ずに自分の手で解けるかを必ず確かめてください。わかっていたつもりでも、いざ自力で解くと解法を思い出せないこともあります。復習は、十分に時間をかけて記憶の新しいうちに行うことが大切です。
方法② 頭の中だけで考えず、書き出すことも大切
条件の中から確実にいえることを、もれなくダブりなく考えていくことが求められています。こうした能力は、俯瞰的に全体構造を考えることにもつながりますから、公務員の実務においても、要求されていることです。
筋道立てて考えていくためにも、効率よくメモ書きも活用していきたいです。そして、図形の問題では、よくわからないときは、実際に作業をしてみることも大切です。たとえば、立方体の展開図でどの辺が重なるか、図形を回転させたときに軌跡がどうなるか、立体を切断したときに切り口がどのようになるかなど、頭の中でわかりにくいときは、具体的に手を動かしたり、工作してみることも理解を深めていくことに大切なことです。
方法③ どんどん演習を重ねる
判断推理は、思考の途中過程も大切です。演習するときには、必ず、ノート、ルーズリーフなどに、途中の思考過程を残しておきましょう。途中で行き詰まったら、何が課題であったかを分析して、最後まで解けたとしても、解説の解法と比較して、より自分にとってベストの解法がないか探究していくとよいです。
問題演習では、時間を計るようにしましょう。解けたとしても、時間のかけすぎはNGです。そして、理解度を〇、△、×のようにメモしておくことも、復習のときに役立ちます。
最初のうちは、自分の受験先の頻度を気にしすぎないことも大切です。まずは、分野ごとの穴をなるべく作らず、それぞれの単元の基礎~標準の問題ができるようにしていきましょう。過去問演習を始める頃からは、頻度や自分自身の得意・不得意を意識しながら、演習をさらに進めていきます。
まとめ
これまで読んでいただき、数的処理・・・判断推理苦手かも。不安と思った方も多いかもしれません。
公務員試験対策を始めたばかりの合格者の多くも同じような状況です。数的処理はどんどん解くことが大切です。解いて解いて、自分自身の不得意を意識しながら対策をしていけば、いつしか身につくものです。
LECでは数的処理が苦手という受験生の声にこたえてインプットはもちろんアウトプット講座まで段階的に受講できる講座をご用意しています。
記事を読んで苦手かも・・・と思った方も思った方も安心してLECの公務員試験対策で頑張りましょう!

- 監修者:志村信幸LEC専任講師
- 10年以上私立中学・高等学校にて数学を担当し、2015年よりLECにて数的処理をはじめ様々な教養科目を担当。
志村信幸LEC専任講師