更新日:2024年8月5日


- 監修者:LEC実力派の講師陣
- LECは公務員試験の指導実績30年以上!
公務員試験を知りつくしたプロ!LEC講師陣が全国で公務員を目指す受験生のために丁寧に指導。
経験豊富な受験指導のプロが受験生の疑問や悩み・不安を解消し、最終合格・内定まで、完全サポートしていきます。
合格に導く実力の講師陣
「数的処理」とは
「数的処理」とは、公務員試験の教養試験で出題される科目です。
数学的・算術的な思考力・推理力を問う問題群であり、「判断推理」「数的推理」「資料解釈」「空間把握」の4つの分野に細分化されます。
公務員試験の教養試験は、「知識分野」と「知能分野」のふたつで構成されます。
数的処理は後者の「知能分野」に属する科目です。多くの官公庁・地方自治体が実施する教養試験は、知識分野より知能分野を重視する傾向にあり、数的処理の問題も多くを占めます。
「数的処理」の重要性
「数的処理」は、出題数が他の科目と比べて多い科目です。
教養試験はどの職種でも必須とされています。出題数が多く、さらに必ず出題されるため、「数的処理」の対策はどの試験でも重要となります。
- 公務員試験はどんな科目が出題されるの!?
- 教養科目50問中17問が数的処理で30%以上を占めています!
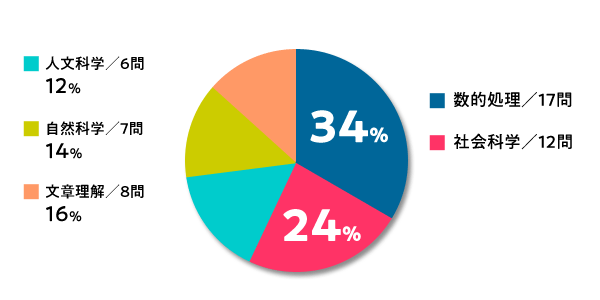 2023年度 地方上級(全国型)試験
2023年度 地方上級(全国型)試験
※教養科目50問、専門科目40問出題全問解答 ※愛媛県(行政事務)採用試験より
公務員試験を受験する上で、数学に苦手意識を抱いている方も多いとは思いますが、対策すれば攻略は可能です。しっかり準備して試験に挑みましょう。
では実際に数的処理の問題に挑戦してみましょう!
- \まずはここからスタート!/
- 資料を請求する
正解の数でチェック!公務員への道
以下に出題されている「数的処理」の5問を解いて、正解の数で公務員への道が開けているかアドバイスいたします!
問1.
ある集団について調査をしたところ次のア~エのことがわかった。ここから確実にいえるのはどれか。
- ア 英語が話せる人は旅行が好きである。
- イ 音楽が好きな人はピアノがひけ、英語も話せる。
- ウ ピアノがひけない人はパソコンができる。
- エ 旅行が好きな人やパソコンができない人は料理が得意である。
選択肢
- 英語が話せる人はピアノがひける。
- 旅行が好きではない人はパソコンができる。
- 音楽が好きな人は料理が得意である。
- パソコンができる人は旅行が好きである。
- 料理が得意でない人はピアノがひけない。
- 解答・解説を見る
-
問1.解答・解説
正解は肢3
各条件を論理式で表すと次のようになります。

これらをひとつにまとめると、以下のようになります。
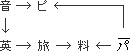
各選択肢を論理式にすると次のようになります。

よって、正解は肢3となります。
※1 論理式では、矢印の方向にたどれると正しくいえることだということになります。
※2 対遇とはある論理式が正しいとしてその裏側で正しくいえることです。
問2.
9個の指輪があり、1個だけが本物で、残りの8個が偽物であることが分かっている。また、外見で本物と偽物の差はないが、重さは本物が少しだけ重いということも分かっている。
このとき、上皿天秤を用いて、本物を確実に見つけ出すためには、最低何回量る必要があるか。
ただし、偽物の重さはすべて等しいとする。
選択肢
- 1回
- 2回
- 3回
- 4回
- 5回
- 解答・解説を見る
-
問2.解答・解説
正解は肢2
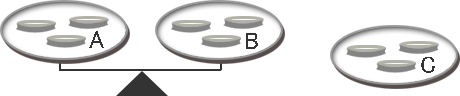
まず9個の指輪を3個ずつ3等分し、それぞれをA、B、Cとおきます。

そして、AとBを上皿天秤にのせます。
1.AとBが同じ重さであり、釣り合った場合
本物はCの中にあるため、Cの3個のうちの2個を天秤に乗せます。 そして、重かった方が本物、または同じ重さなら乗せなかった1個が本物です。 したがって、2回量る必要があります。
2.AとBのどちらかが重い場合
重かった方が本物であるため、重かった方の3個のうちの2個を天秤に乗せます。そして、重かった方が本物、または同じ重さなら乗せなかった1個が本物です。したがって、2回量る必要があります。よって、正解は肢2ということになります。

問3.
東京を「5D、3A、2B、5H、3A」、札幌を「1C、3D、5F、?、5I」、仙台を「4C、1K、1D、#、2A」と表せるとき、「4F、#、3D、3F、?」で表される都市のある県はどれか。
選択肢
- 青森県
- 群馬県
- 愛知県
- 鳥取県
- 大分県
- 解答・解説を見る
-
問3.解答・解説
正解は肢5
例題の条件をひらがなにし、暗号との対応関係をみると、
とうきょう → 「5D、3A、2B、5H、3A」
さっぽろ → 「1C、3D、5F、?、5I」
せんだい → 「4C、1K、1D、#、2A」となり、ひらがな1文字と数字とローマ字の一組が対応していると考えられます。このことから、カナ(五十音表)の暗号であるとわかります。
また、数字は1~5、ローマ字はA~Kが使われているので、数字が段を、ローマ字が行を表していると考えられます。
そして、?は「半濁音」、#は「濁音」を意味すると思われます。
ここで、50音表を作成すると以下のようになります。A B C D E F G H I J K 1 あ か さ た な は ま や ら わ ん 2 い き し ち に ひ み り 3 う く す つ ぬ ふ む ゆ る 4 え け せ て ね へ め れ 5 お こ そ と の ほ も よ ろ を 以上から、設問の暗号文を解読すると「べっぷ(別府)」となり、別府は大分県にありますから、正解は肢5となります。
問4.
A、B、C、Dの4人が縦一列に並んでいる。この4人に白い帽子4つ、ピンクの帽子3つのうちから1つを選んでかぶせることにする。
4人はAを先頭にA~Dの順に並んでおり、自分より前に並んでいる人の帽子の色は見分けられるが、自分を含め自分より後ろの人の帽子の色はわからないものとする。D、C、Bの順に自分の帽子の色がわかるかどうか尋ねたところ、3人のいずれも「わからない」と答えた。
これを聞いていたAに同様の質問をしたところ、Aは自分の帽子の色が「わかった」と答えた。A~Dの帽子の色としてありうるのはどれか。
ただし、4人は用意されていた帽子の色と数の内訳を知っていたものとする。
選択肢
- (A)ピンク (B)ピンク (C)ピンク (D)白
- (A)白 (B)ピンク (C)白 (D)ピンク
- (A)ピンク (B)ピンク (C)白 (D)ピンク
- (A)ピンク (B)白 (C)白 (D)白
- (A)ピンク (B)白 (C)ピンク (D)白
- 解答・解説を見る
-
問4.解答・解説
正解は肢2
Dが自分の帽子の色がわかるのは、A、B、Cの3人がピンクの帽子をかぶっている場合だけです。
この場合、Dの帽子の色は白です。
Dは自分の帽子の色がわからなかったのですから、A、B、Cの3人全員がピンクの帽子をかぶっているということはありえません。
つまり、A、B、Cのなかに、少なくとも1人は白の帽子をかぶっている人がいるということになります。
Dの「わからない」という発言を聞いたCが、自分の帽子の色がわかるのは、A、Bの2人がピンクの帽子をかぶっている場合のみです。この場合、Cの帽子の色は白です。
しかし、Cは自分の帽子の色がわからなかったのですから、A、B2人ともがピンクの帽子をかぶっているということはありえません。
つまり、A、Bの少なくとも1人は白の帽子をかぶっていることになります。
D、Cの「わからない」という発言を聞いたBが、自分の帽子の色がわかるのは、Aがピンクの帽子をかぶっている場合のみです。この場合、Bの帽子の色は白です。
しかし、Bは自分の帽子の色がわからなかったのですから、Aは白の帽子をかぶっていることになります。 以上より、D、C、Bの「わからない」という発言を聞いて、Aは自分の帽子の色が白であるとわかったはずです。Aの帽子の色が白であるのは肢2のみですから、正解は肢2ということになります。
問5.
AとBは同一地点から30km先の目的地に向けて出発することにした。
AはBより15分早く自転車で出発したが、移動の途中でバイクに乗ったBに追い越され、結局、AはBより目的地に10分遅れて到着することとなった。
Bのバイクの速さがAの自転車の速さの1.5倍であったとするとAの速さは時速何kmか。
ただし、2人とも同じ経路を終始一定の速さで走り続けたものとする。
選択肢
- 時速12km
- 時速16km
- 時速20km
- 時速24km
- 時速28km
- 解答・解説を見る
-
問5.解答・解説
正解は肢4
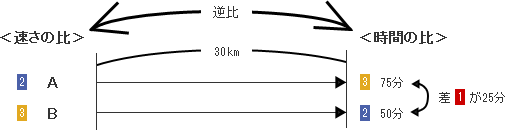
AはBよりも15分早く出発したが、AはBより10分遅れて到着しています。ということは、AはBよりも25分長く走っていることになります。
ここで「2人の走った距離が同じなら、時間と速さは逆比例する。」という公式を知っていると答えが出せます。AとBが走った距離は同じ30㎞ですから、2人がこの30㎞を走るのに何分かかったかということと、2人の走る速さが時速何kmかということが、逆比例の関係だということになります。
そうすると、AとBの走る速さの比率は、BがAの1.5倍の速さなのですから、A対Bが、
 対
対  ということになります。したがって、AとBが、30㎞走るのにかかった時間の比率は、、A対Bが、
ということになります。したがって、AとBが、30㎞走るのにかかった時間の比率は、、A対Bが、  対
対  ということになります。この
ということになります。この  と
と  という比の差である
という比の差である  が具体的には25分なのですから、
が具体的には25分なのですから、  は75分でAは75分かかった、
は75分でAは75分かかった、  は50分でBは50分かかったことになります。
は50分でBは50分かかったことになります。結局、Aは30㎞を75分つまり
 時間かけて走ったことになるので、Aの速さは‥
時間かけて走ったことになるので、Aの速さは‥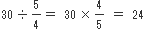
よって、正解は肢4となります。
結果は・・・?
正解が1問以下

正解できなくて当然、はじめて触れる問題です。
これからLECのコースを受講して合格のチャンスをつかみましょう!!